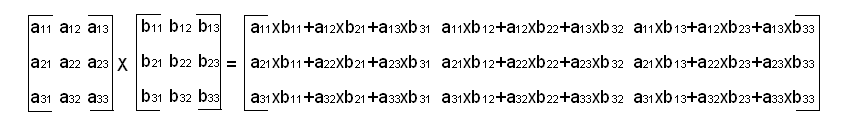CMSIS-DSP  
CMSIS DSP Software Library
 
Loading...
Searching...
No Matches
Functions
Matrix Multiplication
Matrix Functions

Functions

arm_status arm_mat_mult_f16 (const arm_matrix_instance_f16 *pSrcA, const arm_matrix_instance_f16 *pSrcB, arm_matrix_instance_f16 *pDst)
 Floating-point matrix multiplication.
 
arm_status arm_mat_mult_f32 (const arm_matrix_instance_f32 *pSrcA, const arm_matrix_instance_f32 *pSrcB, arm_matrix_instance_f32 *pDst)
 Floating-point matrix multiplication.
 
arm_status arm_mat_mult_f64 (const arm_matrix_instance_f64 *pSrcA, const arm_matrix_instance_f64 *pSrcB, arm_matrix_instance_f64 *pDst)
 Floating-point matrix multiplication.
 
arm_status arm_mat_mult_fast_q15 (const arm_matrix_instance_q15 *pSrcA, const arm_matrix_instance_q15 *pSrcB, arm_matrix_instance_q15 *pDst, q15_t *pState)
 Q15 matrix multiplication (fast variant).
 
arm_status arm_mat_mult_fast_q31 (const arm_matrix_instance_q31 *pSrcA, const arm_matrix_instance_q31 *pSrcB, arm_matrix_instance_q31 *pDst)
 Q31 matrix multiplication (fast variant).
 
arm_status arm_mat_mult_opt_q31 (const arm_matrix_instance_q31 *pSrcA, const arm_matrix_instance_q31 *pSrcB, arm_matrix_instance_q31 *pDst, q31_t *pState)
 Q31 matrix multiplication.
 
arm_status arm_mat_mult_q15 (const arm_matrix_instance_q15 *pSrcA, const arm_matrix_instance_q15 *pSrcB, arm_matrix_instance_q15 *pDst, q15_t *pState)
 Q15 matrix multiplication.
 
arm_status arm_mat_mult_q31 (const arm_matrix_instance_q31 *pSrcA, const arm_matrix_instance_q31 *pSrcB, arm_matrix_instance_q31 *pDst)
 Q31 matrix multiplication.
 
arm_status arm_mat_mult_q7 (const arm_matrix_instance_q7 *pSrcA, const arm_matrix_instance_q7 *pSrcB, arm_matrix_instance_q7 *pDst, q7_t *pState)
 Q7 matrix multiplication.
 

Description

Multiplies two matrices.

Multiplication of two 3x3 matrices:

\[ \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \\ \end{pmatrix} \begin{pmatrix} b_{1,1} & b_{1,2} & b_{1,3} \\ b_{2,1} & b_{2,2} & b_{2,3} \\ b_{3,1} & b_{3,2} & b_{3,3} \\ \end{pmatrix} = \begin{pmatrix} a_{1,1} b_{1,1}+a_{1,2} b_{2,1}+a_{1,3} b_{3,1} & a_{1,1} b_{1,2}+a_{1,2} b_{2,2}+a_{1,3} b_{3,2} & a_{1,1} b_{1,3}+a_{1,2} b_{2,3}+a_{1,3} b_{3,3} \\ a_{2,1} b_{1,1}+a_{2,2} b_{2,1}+a_{2,3} b_{3,1} & a_{2,1} b_{1,2}+a_{2,2} b_{2,2}+a_{2,3} b_{3,2} & a_{2,1} b_{1,3}+a_{2,2} b_{2,3}+a_{2,3} b_{3,3} \\ a_{3,1} b_{1,1}+a_{3,2} b_{2,1}+a_{3,3} b_{3,1} & a_{3,1} b_{1,2}+a_{3,2} b_{2,2}+a_{3,3} b_{3,2} & a_{3,1} b_{1,3}+a_{3,2} b_{2,3}+a_{3,3} b_{3,3} \\ \end{pmatrix} \]

Matrix multiplication is only defined if the number of columns of the first matrix equals the number of rows of the second matrix. Multiplying an M x N matrix with an N x P matrix results in an M x P matrix. When matrix size checking is enabled, the functions check: (1) that the inner dimensions of pSrcA and pSrcB are equal; and (2) that the size of the output matrix equals the outer dimensions of pSrcA and pSrcB.

Multiplies two matrices.

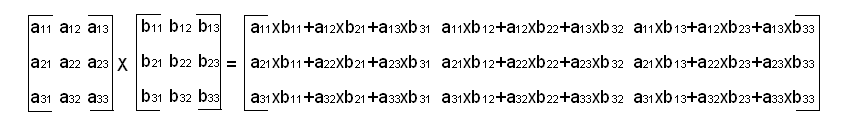
Multiplication of two 3 x 3 matrices

Matrix multiplication is only defined if the number of columns of the first matrix equals the number of rows of the second matrix. Multiplying an M x N matrix with an N x P matrix results in an M x P matrix. When matrix size checking is enabled, the functions check: (1) that the inner dimensions of pSrcA and pSrcB are equal; and (2) that the size of the output matrix equals the outer dimensions of pSrcA and pSrcB.

Function Documentation

◆ arm_mat_mult_f16()

arm_status arm_mat_mult_f16 ( const arm_matrix_instance_f16 *  pSrcA,
const arm_matrix_instance_f16 *  pSrcB,
arm_matrix_instance_f16 *  pDst 
)

Floating-point matrix multiplication.

Parameters
[in]*pSrcApoints to the first input matrix structure
[in]*pSrcBpoints to the second input matrix structure
[out]*pDstpoints to output matrix structure
Returns
The function returns either ARM_MATH_SIZE_MISMATCH or ARM_MATH_SUCCESS based on the outcome of size checking.

◆ arm_mat_mult_f32()

arm_status arm_mat_mult_f32 ( const arm_matrix_instance_f32 *  pSrcA,
const arm_matrix_instance_f32 *  pSrcB,
arm_matrix_instance_f32 *  pDst 
)

Floating-point matrix multiplication.

Parameters
[in]*pSrcApoints to the first input matrix structure
[in]*pSrcBpoints to the second input matrix structure
[out]*pDstpoints to output matrix structure
Returns
The function returns either ARM_MATH_SIZE_MISMATCH or ARM_MATH_SUCCESS based on the outcome of size checking.

◆ arm_mat_mult_f64()

arm_status arm_mat_mult_f64 ( const arm_matrix_instance_f64 *  pSrcA,
const arm_matrix_instance_f64 *  pSrcB,
arm_matrix_instance_f64 *  pDst 
)

Floating-point matrix multiplication.

Parameters
[in]*pSrcApoints to the first input matrix structure
[in]*pSrcBpoints to the second input matrix structure
[out]*pDstpoints to output matrix structure
Returns
The function returns either ARM_MATH_SIZE_MISMATCH or ARM_MATH_SUCCESS based on the outcome of size checking.

◆ arm_mat_mult_fast_q15()

arm_status arm_mat_mult_fast_q15 ( const arm_matrix_instance_q15 *  pSrcA,
const arm_matrix_instance_q15 *  pSrcB,
arm_matrix_instance_q15 *  pDst,
q15_t *  pState 
)

Q15 matrix multiplication (fast variant).

Q15 matrix multiplication (fast variant) for Cortex-M3 and Cortex-M4.

Parameters
[in]pSrcApoints to the first input matrix structure
[in]pSrcBpoints to the second input matrix structure
[out]pDstpoints to output matrix structure
[in]pStatepoints to the array for storing intermediate results
Returns
execution status
Scaling and Overflow Behavior
The difference between the function arm_mat_mult_q15() and this fast variant is that the fast variant use a 32-bit rather than a 64-bit accumulator. The result of each 1.15 x 1.15 multiplication is truncated to 2.30 format. These intermediate results are accumulated in a 32-bit register in 2.30 format. Finally, the accumulator is saturated and converted to a 1.15 result.
The fast version has the same overflow behavior as the standard version but provides less precision since it discards the low 16 bits of each multiplication result. In order to avoid overflows completely the input signals must be scaled down. Scale down one of the input matrices by log2(numColsA) bits to avoid overflows, as a total of numColsA additions are computed internally for each output element.
Remarks
Refer to arm_mat_mult_q15() for a slower implementation of this function which uses 64-bit accumulation to provide higher precision.

◆ arm_mat_mult_fast_q31()

arm_status arm_mat_mult_fast_q31 ( const arm_matrix_instance_q31 *  pSrcA,
const arm_matrix_instance_q31 *  pSrcB,
arm_matrix_instance_q31 *  pDst 
)

Q31 matrix multiplication (fast variant).

Q31 matrix multiplication (fast variant) for Cortex-M3 and Cortex-M4.

Parameters
[in]pSrcApoints to the first input matrix structure
[in]pSrcBpoints to the second input matrix structure
[out]pDstpoints to output matrix structure
Returns
execution status
Scaling and Overflow Behavior
The difference between the function arm_mat_mult_q31() and this fast variant is that the fast variant use a 32-bit rather than a 64-bit accumulator. The result of each 1.31 x 1.31 multiplication is truncated to 2.30 format. These intermediate results are accumulated in a 32-bit register in 2.30 format. Finally, the accumulator is saturated and converted to a 1.31 result.
The fast version has the same overflow behavior as the standard version but provides less precision since it discards the low 32 bits of each multiplication result. In order to avoid overflows completely the input signals must be scaled down. Scale down one of the input matrices by log2(numColsA) bits to avoid overflows, as a total of numColsA additions are computed internally for each output element.
Remarks
Refer to arm_mat_mult_q31() for a slower implementation of this function which uses 64-bit accumulation to provide higher precision.

◆ arm_mat_mult_opt_q31()

arm_status arm_mat_mult_opt_q31 ( const arm_matrix_instance_q31 *  pSrcA,
const arm_matrix_instance_q31 *  pSrcB,
arm_matrix_instance_q31 *  pDst,
q31_t *  pState 
)

Q31 matrix multiplication.

Parameters
[in]pSrcApoints to the first input matrix structure
[in]pSrcBpoints to the second input matrix structure
[out]pDstpoints to output matrix structure
[in]pStatepoints to the array for storing intermediate results
Returns
execution status
Scaling and Overflow Behavior
The function is implemented using an internal 64-bit accumulator. The accumulator has a 2.62 format and maintains full precision of the intermediate multiplication results but provides only a single guard bit. There is no saturation on intermediate additions. Thus, if the accumulator overflows it wraps around and distorts the result. The input signals should be scaled down to avoid intermediate overflows. The input is thus scaled down by log2(numColsA) bits to avoid overflows, as a total of numColsA additions are performed internally. The 2.62 accumulator is right shifted by 31 bits and saturated to 1.31 format to yield the final result.
Remarks
Refer to arm_mat_mult_fast_q31() for a faster but less precise implementation of this function.
This function is a faster implementation of arm_mat_mult_q31 for MVE but it is requiring additional storage for intermediate results.

◆ arm_mat_mult_q15()

arm_status arm_mat_mult_q15 ( const arm_matrix_instance_q15 *  pSrcA,
const arm_matrix_instance_q15 *  pSrcB,
arm_matrix_instance_q15 *  pDst,
q15_t *  pState 
)

Q15 matrix multiplication.

Parameters
[in]pSrcApoints to the first input matrix structure
[in]pSrcBpoints to the second input matrix structure
[out]pDstpoints to output matrix structure
[in]pStatepoints to the array for storing intermediate results
Returns
execution status
Scaling and Overflow Behavior
The function is implemented using an internal 64-bit accumulator. The inputs to the multiplications are in 1.15 format and multiplications yield a 2.30 result. The 2.30 intermediate results are accumulated in a 64-bit accumulator in 34.30 format. This approach provides 33 guard bits and there is no risk of overflow. The 34.30 result is then truncated to 34.15 format by discarding the low 15 bits and then saturated to 1.15 format.
Refer to arm_mat_mult_fast_q15() for a faster but less precise version of this function.
pState
pState will contain the transpose of pSrcB

◆ arm_mat_mult_q31()

arm_status arm_mat_mult_q31 ( const arm_matrix_instance_q31 *  pSrcA,
const arm_matrix_instance_q31 *  pSrcB,
arm_matrix_instance_q31 *  pDst 
)

Q31 matrix multiplication.

Parameters
[in]pSrcApoints to the first input matrix structure
[in]pSrcBpoints to the second input matrix structure
[out]pDstpoints to output matrix structure
Returns
execution status
Scaling and Overflow Behavior
The function is implemented using an internal 64-bit accumulator. The accumulator has a 2.62 format and maintains full precision of the intermediate multiplication results but provides only a single guard bit. There is no saturation on intermediate additions. Thus, if the accumulator overflows it wraps around and distorts the result. The input signals should be scaled down to avoid intermediate overflows. The input is thus scaled down by log2(numColsA) bits to avoid overflows, as a total of numColsA additions are performed internally. The 2.62 accumulator is right shifted by 31 bits and saturated to 1.31 format to yield the final result.
Remarks
Refer to arm_mat_mult_fast_q31() for a faster but less precise implementation of this function.

◆ arm_mat_mult_q7()

arm_status arm_mat_mult_q7 ( const arm_matrix_instance_q7 *  pSrcA,
const arm_matrix_instance_q7 *  pSrcB,
arm_matrix_instance_q7 *  pDst,
q7_t *  pState 
)

Q7 matrix multiplication.

Parameters
[in]*pSrcApoints to the first input matrix structure
[in]*pSrcBpoints to the second input matrix structure
[out]*pDstpoints to output matrix structure
[in]*pStatepoints to the array for storing intermediate results (Unused in some versions)
Returns
The function returns either ARM_MATH_SIZE_MISMATCH or ARM_MATH_SUCCESS based on the outcome of size checking.

Scaling and Overflow Behavior:

The function is implemented using a 32-bit internal accumulator saturated to 1.7 format.