Vector Inverse Clarke Transform

Functions
void	arm_inv_clarke_f32 (float32_t Ialpha, float32_t Ibeta, float32_t *pIa, float32_t *pIb)
	Floating-point Inverse Clarke transform.
void	arm_inv_clarke_q31 (q31_t Ialpha, q31_t Ibeta, q31_t *pIa, q31_t *pIb)
	Inverse Clarke transform for Q31 version.

Description

Inverse Clarke transform converts the two-coordinate time invariant vector into instantaneous stator phases.

The function operates on a single sample of data and each call to the function returns the processed output. The library provides separate functions for Q31 and floating-point data types.

Algorithm

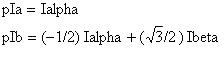
where pIa and pIb are the instantaneous stator phases and Ialpha and Ibeta are the two coordinates of time invariant vector.

Fixed-Point Behavior

Care must be taken when using the Q31 version of the Clarke transform. In particular, the overflow and saturation behavior of the accumulator used must be considered. Refer to the function specific documentation below for usage guidelines.

Function Documentation

arm_inv_clarke_f32()

void arm_inv_clarke_f32	(	float32_t	Ialpha,
		float32_t	Ibeta,
		float32_t *	pIa,
		float32_t *	pIb
	)

Floating-point Inverse Clarke transform.

Parameters

[in]	Ialpha	input two-phase orthogonal vector axis alpha
[in]	Ibeta	input two-phase orthogonal vector axis beta
[out]	pIa	points to output three-phase coordinate a
[out]	pIb	points to output three-phase coordinate b

arm_inv_clarke_q31()

void arm_inv_clarke_q31	(	q31_t	Ialpha,
		q31_t	Ibeta,
		q31_t *	pIa,
		q31_t *	pIb
	)

Inverse Clarke transform for Q31 version.

Parameters

[in]	Ialpha	input two-phase orthogonal vector axis alpha
[in]	Ibeta	input two-phase orthogonal vector axis beta
[out]	pIa	points to output three-phase coordinate a
[out]	pIb	points to output three-phase coordinate b

Scaling and Overflow Behavior

The function is implemented using an internal 32-bit accumulator. The accumulator maintains 1.31 format by truncating lower 31 bits of the intermediate multiplication in 2.62 format. There is saturation on the subtraction, hence there is no risk of overflow.