Functions
void	arm_fir_interpolate_f32 (const arm_fir_interpolate_instance_f32 S, const float32_t pSrc, float32_t *pDst, uint32_t blockSize)
	Processing function for floating-point FIR interpolator. More...

arm_status	arm_fir_interpolate_init_f32 (arm_fir_interpolate_instance_f32 S, uint8_t L, uint16_t numTaps, const float32_t pCoeffs, float32_t *pState, uint32_t blockSize)
	Initialization function for the floating-point FIR interpolator. More...

arm_status	arm_fir_interpolate_init_q15 (arm_fir_interpolate_instance_q15 S, uint8_t L, uint16_t numTaps, const q15_t pCoeffs, q15_t *pState, uint32_t blockSize)
	Initialization function for the Q15 FIR interpolator. More...

arm_status	arm_fir_interpolate_init_q31 (arm_fir_interpolate_instance_q31 S, uint8_t L, uint16_t numTaps, const q31_t pCoeffs, q31_t *pState, uint32_t blockSize)
	Initialization function for the Q31 FIR interpolator. More...

void	arm_fir_interpolate_q15 (const arm_fir_interpolate_instance_q15 S, const q15_t pSrc, q15_t *pDst, uint32_t blockSize)
	Processing function for the Q15 FIR interpolator. More...

void	arm_fir_interpolate_q31 (const arm_fir_interpolate_instance_q31 S, const q31_t pSrc, q31_t *pDst, uint32_t blockSize)
	Processing function for the Q31 FIR interpolator. More...

Description

These functions combine an upsampler (zero stuffer) and an FIR filter. They are used in multirate systems for increasing the sample rate of a signal without introducing high frequency images. Conceptually, the functions are equivalent to the block diagram below:

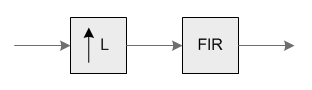
Components included in the FIR Interpolator functions

After upsampling by a factor of L, the signal should be filtered by a lowpass filter with a normalized cutoff frequency of 1/L in order to eliminate high frequency copies of the spectrum. The user of the function is responsible for providing the filter coefficients.

The FIR interpolator functions provided in the CMSIS DSP Library combine the upsampler and FIR filter in an efficient manner. The upsampler inserts L-1 zeros between each sample. Instead of multiplying by these zero values, the FIR filter is designed to skip them. This leads to an efficient implementation without any wasted effort. The functions operate on blocks of input and output data. pSrc points to an array of blockSize input values and pDst points to an array of blockSize*L output values.

The library provides separate functions for Q15, Q31, and floating-point data types.

Algorithm

The functions use a polyphase filter structure:

    y[n] = b[0] * x[n] + b[L]   * x[n-1] + ... + b[L*(phaseLength-1)] * x[n-phaseLength+1]
    y[n+1] = b[1] * x[n] + b[L+1] * x[n-1] + ... + b[L*(phaseLength-1)+1] * x[n-phaseLength+1]
    ...
    y[n+(L-1)] = b[L-1] * x[n] + b[2*L-1] * x[n-1] + ....+ b[L*(phaseLength-1)+(L-1)] * x[n-phaseLength+1]

This approach is more efficient than straightforward upsample-then-filter algorithms. With this method the computation is reduced by a factor of 1/L when compared to using a standard FIR filter.

pCoeffs points to a coefficient array of size numTaps. numTaps must be a multiple of the interpolation factor L and this is checked by the initialization functions. Internally, the function divides the FIR filter's impulse response into shorter filters of length phaseLength=numTaps/L. Coefficients are stored in time reversed order.

    {b[numTaps-1], b[numTaps-2], b[N-2], ..., b[1], b[0]}

pState points to a state array of size blockSize + phaseLength - 1. Samples in the state buffer are stored in the order:

   {x[n-phaseLength+1], x[n-phaseLength], x[n-phaseLength-1], x[n-phaseLength-2]....x[0], x[1], ..., x[blockSize-1]}

: The state variables are updated after each block of data is processed, the coefficients are untouched.

Instance Structure: The coefficients and state variables for a filter are stored together in an instance data structure. A separate instance structure must be defined for each filter. Coefficient arrays may be shared among several instances while state variable array should be allocated separately. There are separate instance structure declarations for each of the 3 supported data types.

Initialization Functions

There is also an associated initialization function for each data type. The initialization function performs the following operations:

Sets the values of the internal structure fields.
Zeros out the values in the state buffer.
Checks to make sure that the length of the filter is a multiple of the interpolation factor. To do this manually without calling the init function, assign the follow subfields of the instance structure: L (interpolation factor), pCoeffs, phaseLength (numTaps / L), pState. Also set all of the values in pState to zero.

Use of the initialization function is optional. However, if the initialization function is used, then the instance structure cannot be placed into a const data section. To place an instance structure into a const data section, the instance structure must be manually initialized. The code below statically initializes each of the 3 different data type filter instance structures

    arm_fir_interpolate_instance_f32 S = {L, phaseLength, pCoeffs, pState};
    arm_fir_interpolate_instance_q31 S = {L, phaseLength, pCoeffs, pState};
    arm_fir_interpolate_instance_q15 S = {L, phaseLength, pCoeffs, pState};

: where L is the interpolation factor; phaseLength=numTaps/L is the length of each of the shorter FIR filters used internally, pCoeffs is the address of the coefficient buffer; pState is the address of the state buffer. Be sure to set the values in the state buffer to zeros when doing static initialization.

Fixed-Point Behavior: Care must be taken when using the fixed-point versions of the FIR interpolate filter functions. In particular, the overflow and saturation behavior of the accumulator used in each function must be considered. Refer to the function specific documentation below for usage guidelines.

Function Documentation

◆ arm_fir_interpolate_f32()

void arm_fir_interpolate_f32	(	const arm_fir_interpolate_instance_f32 *	S,
		const float32_t *	pSrc,
		float32_t *	pDst,
		uint32_t	blockSize
	)

Processing function for the floating-point FIR interpolator.

Parameters

[in]	S	points to an instance of the floating-point FIR interpolator structure
[in]	pSrc	points to the block of input data
[out]	pDst	points to the block of output data
[in]	blockSize	number of samples to process

Returns: none

◆ arm_fir_interpolate_init_f32()

arm_status arm_fir_interpolate_init_f32	(	arm_fir_interpolate_instance_f32 *	S,
		uint8_t	L,
		uint16_t	numTaps,
		const float32_t *	pCoeffs,
		float32_t *	pState,
		uint32_t	blockSize
	)

Parameters

[in,out]	S	points to an instance of the floating-point FIR interpolator structure
[in]	L	upsample factor
[in]	numTaps	number of filter coefficients in the filter
[in]	pCoeffs	points to the filter coefficient buffer
[in]	pState	points to the state buffer
[in]	blockSize	number of input samples to process per call

Returns

execution status

ARM_MATH_SUCCESS : Operation successful
ARM_MATH_ARGUMENT_ERROR : filter length numTaps is not a multiple of the interpolation factor L

Details

pCoeffs points to the array of filter coefficients stored in time reversed order:

    {b[numTaps-1], b[numTaps-2], b[numTaps-2], ..., b[1], b[0]}

: The length of the filter numTaps must be a multiple of the interpolation factor L.

: pState points to the array of state variables. pState is of length (numTaps/L)+blockSize-1 words where blockSize is the number of input samples processed by each call to arm_fir_interpolate_f32().

◆ arm_fir_interpolate_init_q15()

arm_status arm_fir_interpolate_init_q15	(	arm_fir_interpolate_instance_q15 *	S,
		uint8_t	L,
		uint16_t	numTaps,
		const q15_t *	pCoeffs,
		q15_t *	pState,
		uint32_t	blockSize
	)

Parameters

[in,out]	S	points to an instance of the Q15 FIR interpolator structure
[in]	L	upsample factor
[in]	numTaps	number of filter coefficients in the filter
[in]	pCoeffs	points to the filter coefficient buffer
[in]	pState	points to the state buffer
[in]	blockSize	number of input samples to process per call

Returns

execution status

ARM_MATH_SUCCESS : Operation successful
ARM_MATH_ARGUMENT_ERROR : filter length numTaps is not a multiple of the interpolation factor L

Details

pCoeffs points to the array of filter coefficients stored in time reversed order:

    {b[numTaps-1], b[numTaps-2], b[numTaps-2], ..., b[1], b[0]}

The length of the filter numTaps must be a multiple of the interpolation factor L.

: pState points to the array of state variables. pState is of length (numTaps/L)+blockSize-1 words where blockSize is the number of input samples processed by each call to arm_fir_interpolate_q15().

◆ arm_fir_interpolate_init_q31()

arm_status arm_fir_interpolate_init_q31	(	arm_fir_interpolate_instance_q31 *	S,
		uint8_t	L,
		uint16_t	numTaps,
		const q31_t *	pCoeffs,
		q31_t *	pState,
		uint32_t	blockSize
	)

Parameters

[in,out]	S	points to an instance of the Q31 FIR interpolator structure
[in]	L	upsample factor
[in]	numTaps	number of filter coefficients in the filter
[in]	pCoeffs	points to the filter coefficient buffer
[in]	pState	points to the state buffer
[in]	blockSize	number of input samples to process per call

Returns

execution status

ARM_MATH_SUCCESS : Operation successful
ARM_MATH_ARGUMENT_ERROR : filter length numTaps is not a multiple of the interpolation factor L

Details

pCoeffs points to the array of filter coefficients stored in time reversed order:

    {b[numTaps-1], b[numTaps-2], b[numTaps-2], ..., b[1], b[0]}

The length of the filter numTaps must be a multiple of the interpolation factor L.

: pState points to the array of state variables. pState is of length (numTaps/L)+blockSize-1 words where blockSize is the number of input samples processed by each call to arm_fir_interpolate_q31().

◆ arm_fir_interpolate_q15()

void arm_fir_interpolate_q15	(	const arm_fir_interpolate_instance_q15 *	S,
		const q15_t *	pSrc,
		q15_t *	pDst,
		uint32_t	blockSize
	)

Parameters

[in]	S	points to an instance of the Q15 FIR interpolator structure
[in]	pSrc	points to the block of input data
[out]	pDst	points to the block of output data
[in]	blockSize	number of samples to process

Returns: none

Scaling and Overflow Behavior: The function is implemented using a 64-bit internal accumulator. Both coefficients and state variables are represented in 1.15 format and multiplications yield a 2.30 result. The 2.30 intermediate results are accumulated in a 64-bit accumulator in 34.30 format. There is no risk of internal overflow with this approach and the full precision of intermediate multiplications is preserved. After all additions have been performed, the accumulator is truncated to 34.15 format by discarding low 15 bits. Lastly, the accumulator is saturated to yield a result in 1.15 format.

◆ arm_fir_interpolate_q31()

void arm_fir_interpolate_q31	(	const arm_fir_interpolate_instance_q31 *	S,
		const q31_t *	pSrc,
		q31_t *	pDst,
		uint32_t	blockSize
	)

Parameters

[in]	S	points to an instance of the Q31 FIR interpolator structure
[in]	pSrc	points to the block of input data
[out]	pDst	points to the block of output data
[in]	blockSize	number of samples to process

Returns: none

Scaling and Overflow Behavior: The function is implemented using an internal 64-bit accumulator. The accumulator has a 2.62 format and maintains full precision of the intermediate multiplication results but provides only a single guard bit. Thus, if the accumulator result overflows it wraps around rather than clip. In order to avoid overflows completely the input signal must be scaled down by 1/(numTaps/L). since numTaps/L additions occur per output sample. After all multiply-accumulates are performed, the 2.62 accumulator is truncated to 1.32 format and then saturated to 1.31 format.